Binary Search I

Binary search is the fastest way to search elements in sorted static array have time complexities of O(logn). In this article will look a template for doing binary search and then extending that template for variants of binary search problems.

Example

Template for Iterative Binary Search

def binarySearch(nums: List[int], target: int) -> int:
    st, end = 0, len(nums) - 1
    while st <= end:
        mid = st + (end - st)//2
        if nums[mid] == target:
            return mid
        if nums[mid] < target:
            st = mid + 1
        else:
            end = mid - 1
    return -1

Other Examples:

Now based on finding let’s try to see what happens when the while loop completely runs in the problem.

Suppose you have n versions [1, 2, ..., n] and you want to find out the first bad one, which causes all the following ones to be bad.

You are given an API bool isBadVersion(version) which returns whether version is bad. Implement a function to find the first bad version. You should minimize the number of calls to the API.

In this problem as you can see there are only two partitions i.e. Good and Bad versions. So when the mid version is good, it is on the left side of the partition and need to move the start to the mid + 1 and when mid version is bad, it is on the right side of the partition and needs to move to the left.

Important conditions here is what happens when while loop stops i.e. start > end. In such a case start = end + 1, the position of start will the first element of the right parition i.e. first bad version. End will point to the last element in the left partition i.e. last good version. The diagram below shows the end of the while loop. At the end either the mid will be first bad element (right element on the partition), in which case end will become mid - 1 and then only start will increase in further iterations till it becomes mid. Or mid will be the last good element (left element of the partition) in which case start will become mid + 1and end will decrease in further iterations till it reaches start - 1 or left element of the parition.

binary Search end condition

Code for this problem can be given as

def firstBadVersion(n: int) -> int:
    st, end = 1, n
    while st <= end:
        mid = st + (end - st)// 2
        isBad = isBadVersion(mid)
        if isBad: # Belongs to right partition, look to the left by moving end to mid - 1
            end = mid - 1
        else: # Belongs to the left partition, look to the right by moving start to mid + 1 
            st = mid + 1
    return st # return the first bad version.

Once this concept is understood, that at the end of the while loop, start will point to the first element of the right partition and end will point to the last element of left parititon. Then after that the problem becomes all about defining the paritions in the binary search.

Following are some of the examples based on the concept.

This problem is again very similar to the previous problem, just the function to define parition is different.

Search Insert parition

def searchInsert(nums: List[int], target: int) -> int:
    st, end = 0, len(nums) - 1
    while st <= end:
        mid = st + (end - st)//2
        if nums[mid] < target: # If in left parition, move the start to the right
            st = mid + 1
        else: # If in the right parition, move the end to the left
            end = mid - 1
    return st

other similar examples, with similar templates:

Finding the partitions, can be further enhanced to find boundry of two partitions as seen in this problem.

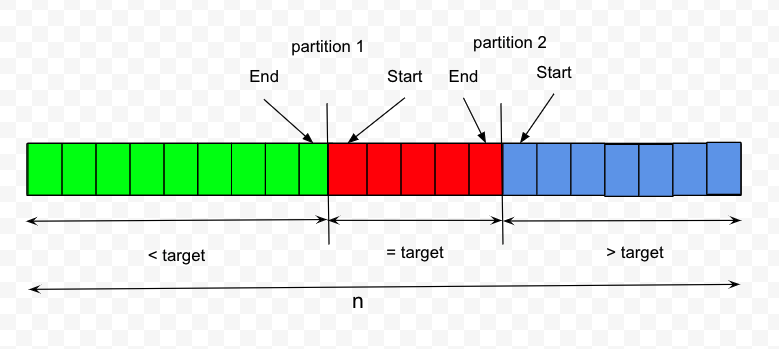
In this problem, looking for start and end indexes for the target value. This can be interpreted as finding two partition boundaries i.e.

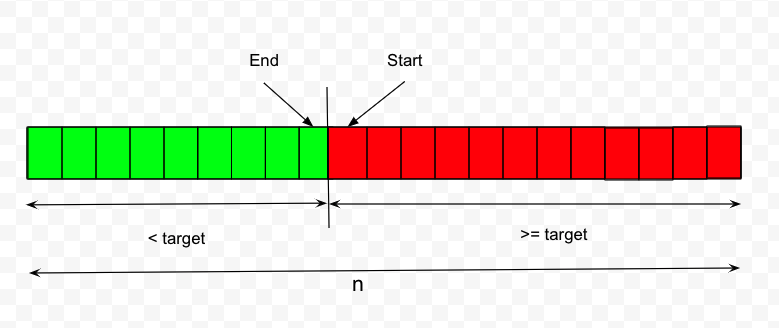
  1. Partition/Boundary 1: Left partition contains all element < target and right partition >= target. In that case the start points to index at the end of the loop to the start of =target partition if valid.
  2. Parititon/Boundary 2: Left partition contains all element <= target and right partition > target. In that case the end points to index at the end of the while loop to the end of =target parition.

Search Two partitions

def searchRange(nums: List[int], target: int) -> List[int]:
    st , end = 0, len(nums) - 1
    while st <= end: # Find partition 1 boundary 1
        mid = st + (end - st)//2
        if nums[mid] < target:
            st = mid + 1
        else:
            end = mid - 1
    if st == len(nums) or nums[st] != target: # If the target is not found
    # Reached end of array as all numbers were smaller than target.
    # Array doesn't have the target number
        return [-1, -1]
    first, end = st, len(nums) - 1
    while st <= end: # Find partition 2 boundary 2
        mid = st + (end - st)//2
        if nums[mid] <= target:
            st = mid + 1
        else:
            end = mid - 1
    return [first, end]

Other similar problem:

Binary Search in a Matrix

def searchMatrix(mat: List[List[int]], target: int) -> bool:
    n, m = len(mat), len(mat[0])
    if n == 0 or m == 0:
        return False
    st, end = 0, n * m - 1 # Take the matrix as single dimension array
    while st <= end:
        mid = st + (end - st) // 2
        r, c = mid//m, mid % m # Convert single dimension field to matrix row and col.
        if mat[r][c] == target:
            return True
        if mat[r][c] < target:
            st = mid + 1
        else:
            end = mid - 1
    return False
comments powered by Disqus