Binary Search II

In the previous article related to binary search, when the element is found and when element is not found in a sorted array. In this article will look at binary search when overall array is exactly not sorted.

Example Problem:

• Peak index in a mountain Array

In this problem, a peak is somewhere middle of the array. All the elements to the left and right of the peak are monotonically decreasing. As you can see array is not exactly sorted in the usual terms here. As described in the previous article, we can find the boundry if we can divide the array in two sections with an invariant. Finding this invariant requires little bit analysis of the problem. Once the invariant is determined the problem is about applying the template to find the boundry.

Such template can be given as.

def binarySearchBoundry(arr: List[int]) -> int:
    st, end = 0, len(arr) - 1 # start, end to the left and right end of the array.
    while st <= end:
        mid = st + (end - st)//2
        if "<left boundry invariant>": # if the mid lies in the left boundary, How that is determined?
            st = mid + 1 # Move the mid to the right side
        else: # Else the mid lies in the right boundary.
            end = mid - 1 # Move the mid to the left side
    return "st/end" # st points to the start of the right boundary, end points to the end of the left boundary"

When the while loop ends the array will be partitioned based on the left and right invariants.

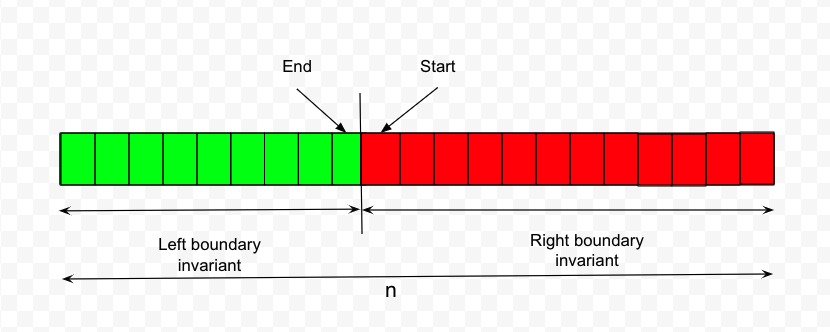
For the peak problem the left invariant can be given as arr[mid] < arr[mid + 1] i.e. every element to the left of the peak if chosen as the peak will be smaller than the next element. And same is not true in the case of the right partition including peak i.e. if any element is chosen from the peak to the right as mid then arr[mid] > arr[mid + 1]. So when the partition is done at the end of the while loop, the start will point to the starting index of the right boundary which will be the peak.

Based on the template above the peak finding code can be written as.

def peakIndexInMountainArray(arr: List[int]) -> int:
    n = len(arr)
    st, end = 0, len(arr) - 1 # Edge case, as the left variant looks as the right element
    while st <= end:
        mid = st + (end - st)//2
        if mid < n - 1 and arr[mid] < arr[mid + 1]: # All the elements to the left of the peak will be smaller than the next element.
            st = mid + 1
        else:
            end = mid - 1
    return st # start points to the starting index of the right boundary, which is peak

Other similar problems:

• find in mountain array

In the above problem, once the peak can be determined using above code and checked for target. Then it is about binary search target to the left increasing partition of the peak and if not found binary search to the right decreasing partition of the peak.

• find peak element

Finding any peak element in the array, in this problem the array is not sorted at all and still to do the problem in O(logn) complexity. We need to apply binary search in the problem. So it is important to understand, that binary search is not just applied in the case of sorted arrays. Problem can also be given as finding any local maximum or any local minimum in an array.

Actually the code of this problem is exactly same as the code for finding when there is just one peak. The idea here is when the mid lands in an ascending region of the peak i.e. where arr[mid] < arr[mid + 1], then there would be a peak on the right side of the region else the peak would be on the left side of the descending region. So eventually it will converge to one of the peaks which is in the middle of ascending and descending region.

Based on the same template, let’s look at other problem.

• Find minimum in rotated sorted array

Finding minimum in a sorted array is a O(1) operation as minimum is at 0 index. Finding minimum in unsorted array is O(n) operation as elements need to be seen atleast once to know the minimum. So in the rotated sorted array, can reduced from O(n) to O(logn) using binary search. Similar to the previous problems, solving it using binary search we can find the parition in the array. So the same template can be used as given above, thing which changes is the paritioning invariant. To come up with the left partitioning invariant nums[mid] > nums[-1], lets draw a diagram of the array.

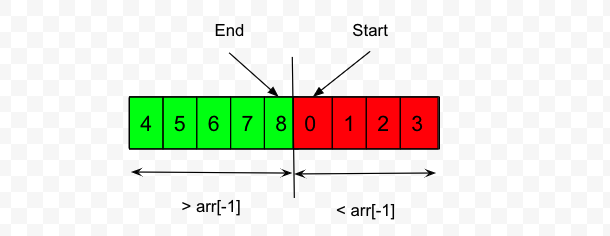
It can be seen that, both the sides of the parition are monotonically increasing from left to right, so that cannot be used as the partitioning function as in the previous problem. But if we look at the left side of the partition it will higher than the last number and in the right side of the partition number will be smaller than the last number. We can use this invariant to add to the template to form the code below.

def findMin(nums: List[int]) -> int:
    n = len(nums)
    st, end = 0 , n - 1
    while st <= end:
        mid = st + (end - st)//2
        if nums[mid] > nums[-1]:
            st = mid + 1
        else:
            end = mid - 1
    return nums[st]

Extension:

• Minimum in sorted rotated array II

In this problem, when the numbers can be repeated the nums[mid] > nums[-1] condition will not able to identify the left partition correctly. As there could be numbers in the start of the array which are equal to nums[-1]. So an easy way to solve the problem is to ignore the numbers in the start of the array which are equal to nums[-1] before running the binary search as given above.

Next Problem:

• Search in rotated sorted array

Based on the rotated sorted array searching a target value, requires more careful evaluation of the partitions. Based on the target value, the left and right parition can change in this problem. There are two possible scenarios:

1. In first scenario target value is smaller or equal than the last value in the array i.e. t <= nums[-1]. In such a case only when the nums[mid] is between the target and last value i.e. t < nums[mid] < nums[-1] then the mid lies in the right of the target value and needs to move left so end=mid-1. In all other cases i.e. nums[mid] > nums[-1] or nums[mid] < t, mid lies to the left of the target value and needs to move to the right by st = mid + 1. This scenario will also be the case, when the array is not rotated as the last index will be highest value.

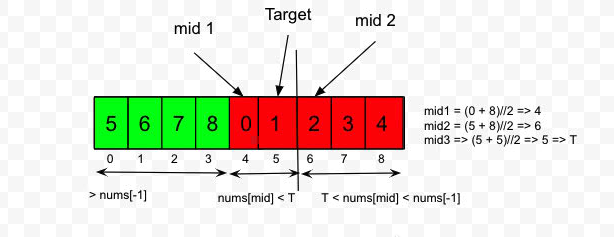
2. In second scenario target value is greater than the last value i.e. t > nums[-1]. In such a case only when the nums[mid] lies in between the last value and target value i.e. nums[-1] < nums[mid] < t then the mid lies in the left of the target value and needs to move right so st = mid + 1. In the other cases i.e. nums[mid] >= t or nums[mid] < nums[-1], mid lies to the right of the target value and needs to move to the left by end = mid - 1.

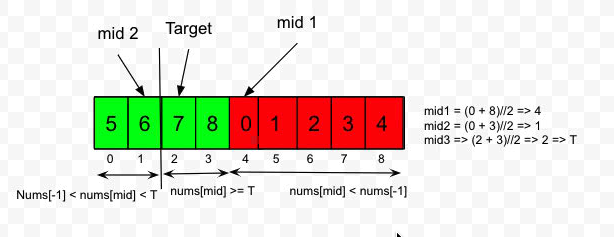
Using these two scenario, code can be performed as a binary search as given below.

def searchInRotated(nums: List[int], t: int) -> int:
    n = len(nums)
    if n == 0:
        return -1
    st, end = 0, n - 1
    while st <= end:
        mid = st + (end - st)//2
        if nums[mid] == t:
            return mid
        if t <= nums[-1]:
            if t < nums[mid] < nums[-1]:
                end = mid - 1
            else:
                st = mid + 1
        else:
            if nums[-1] < nums[mid] < t:
                st = mid + 1
            else:
                end = mid - 1
    return -1

• Search in rotated sorted array II