Directed Graphs

In the previous section on Graphs, discussed about un-directed graphs and applied two graph traversal algorithms dfs and bfs. The problems on undirected are usually more simpler, because the edges in the dfs and bfs tree are very simple in the graphs as there is no direction to the edge. So usually problem are about traversal of the graph or finding a cycle or connected component in graph or a path between two nodes. Usually for these problems either BFS or DFS both give the right solution. In the case of directed graph, the selection of traversal algorithm is also important for the type of problem. For some problems like detecting a cycle or topological sort only DFS algorithm makes sense, whereas shortest path in the graph BFS algorithm makes more sense.

In this post I will discuss about the templates of both DFS and BFS for directed graphs. Also look at some of the problems for directed graphs using these templates.

Overall the structure of solving the directed graph problem will look same, which is:

0. Determine if the given problem is a graph problem, some problems are implicit. Where it is not implicit, mostly in graph problems there would be objects like n people, n cities, n courses and there will be relationship between the objects like dislikes or friendship for people, time or road connection, distance for cities, prerequisites for courses. That should point to the direction of graph people.
1. Build the graph structure, either a adjList or adjMap to store the objects and relationship in form of edges.
2. Determine, what kind of graph it is directed or un-directed, i.e. if there are one way relationships like dislikes, prerequisites the graph is directed, where as relationships like distance are directed.
3. Apply DFS or BFS algorithm based on the graph problem based in the directed graph.
4. Run an outer loop for each of the vertex and run DFS or BFS on each of the vertex based on the graph.

Let’s now look at what problems DFS and BFS can be applied to solve them.

DFS#

The template DFS in the directed graph is based on the template of the undirected as posted in the previous graph. Along with two small changes.

visited = defaultdict(bool)
# dTime refers to discovery time
dTime = defaultdict(int)
# fTime refers to finish time
fTime = defaultdict(int)
timer = 0

def dfs(u: int):
  visited[u] = True
  # record the time/order in which the vertex was added to the recursive call stack
  timer += 1
  dTime[u] = timer
  for v in graph[u]:
    if v not in visited:
      dfs(v)
  # record the time/order in which the vertex pops out of the recursive call stack
  timer += 1
  fTime[u] = timer

# Outer loop to run dfs, on each non visited vertex
for v in graph:
  if v not in visited:
    dfs(v)

Built on the basic template from undirected dfs, recording two extra values in dTime and fTime map.

1. The time/order in which the vertex gets added to the recursive call stack when discovered, which is being stored in dTime. This map stores value of the counter timer after incrementing it. The value dTime of a vertex gives the order in comparison to the rest of the vertices when they are discovered.

2. The map fTime stores the time/order in which the vertex gets popped out of the call stack as they get finished. This is done after recursively calling all the neighbors of the vertex and finishing the work on the vertex. This is again done by incrementing the timer and then storing the value of timer in the fTime.

For Reference this is very well explained in the CLRS book, in Chapter Elementary Graph Algorithms in section of depth first search. It would be good to go over that section. The template above is just a python code of the algorithm in the book.

Recording these actions help, to determine the type of edge connecting the vertex in the dfs tree of the graph. Let’s see how. I have taken the same graph as the CLRS book.

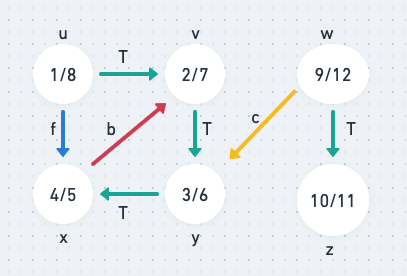
In this graph, the dfs basically starts with vertex u. The order of each vertex i.e. discovery/finish order are listed for each vertex. As the recursive calls progresses each edge in the graph is labelled as

1. Tree Edge (Green color) in the picture above. The tree edge denotes the edges following the recursive call stack. These edges have parent to child relationship, where the child is getting discovered first time when accessed from parent.
2. Back Edge (Red Color), these are edge from descendant to the ancestor in the recursive call stack or depth-first tree.
3. Forward Edge (Blue Color), there are also edge from ancestor to descendant which are non tree and connected to vertex which has already finished and returned.
4. Cross Edge (Yellow Color), all other edges and no relationship can be established here. They can either go from vertices in the same depth first tree if there is no ancestor relationship between two vertices or it can be edge between two depth first tree.

The dfs tree exploration gives few interesting properties with the timer.

Parentheses property#

Let’s say for each vertex discovery time is denoted by open parentheses { and finish Time is denoted by closing parentheses }. Then we can use the dTime and fTime of vertices to get the properties below.

1. Node connected with back edge, for example x -> v, the discovery time and finish time of x will contained entirely within discovery time of v i.e. dTime[v] < dTime[x] < fTime[x] < fTime[v]. And v will be an ancestor or x.
2. Node connected with Tree edge or Forward edge for example u -> v or u -> x, the discovery time and finish time of the descendant in this case v, x will always be contained by the discovery and finish time of the ancestor i.e. u. i.e. dTime[u] < dTime[x] < fTime[x] < fTime[u] and dTime[u] < dTime[v] < fTime[v] < fTime[u]

Basically from 1 and 2, it can be said that for back, forward and tree edges ancestor discovery and finish time will always contain the descendants discovery and finish time. Or descendants will always finish before their ancestor. In other words using the parentheses it will look something like { {} } where the outer parentheses are for the ancestor, and inner parentheses block is for the descendant.

3. The vertex of the cross edges don’t have ancestor and descendant relationship, their discovery time will disjoint sets. For example for cross edge w -> y [dTime[y]/fTime[y]] < [dTime[w]/fTime[y]], basically there is no overlap like in the case of ancestor and descendant relationship. Using the parentheses to replace the dTime and fTime for the vertices of cross edge, it will look like {} {}.

Detect cycle#

4. Only a back edge to the ancestor will lead to a cycle in the graph. So to find if there is a cycle in the graph find if there is a back edge. This edge can be determined very easily by checking if the visited neighbor finish time not present in fTime during recursion. This is because finish Time of the ancestor will be greater than the descendant. As descendant is processing it visits a vertex already visited with no finish time pointing that the vertex is an ancestor.

The above template can be updated in the clause when neighbor is already visited, to detect cycles in the directed graph as:

visited = defaultdict(bool)
# dTime refers to discovery time
dTime = defaultdict(int)
# fTime refers to finish time
fTime = defaultdict(int)
timer = 0

# returns True if there is a cycle in the graph
def dfs(u: int)->bool:
  visited[u] = True
  # record the time/order in which the vertex was added to the recursive call stack
  timer += 1
  dTime[u] = timer
  for v in graph[u]:
    if v not in visited:
      # if the descendants return a cycle, return a cycle found, no need to continue further.
      if dfs(v):
        return True
    else:
      # v node already visited, now checking if it is a ancestor in dfs tree, by checking if it is finished
      if v not in fTime:
        # back edge found
        return True
  # record the time/order in which the vertex pops out of the recursive call stack
  timer += 1
  fTime[u] = timer
  return False

# Outer loop to run dfs on each non visited vertex, if cycle return True
for v in graph:
  if v not in visited:
    if dfs(v):
      return True
return False

Topological Sort#

5. If there are no cycles in the directed graph, i.e. there are no back edges in the graph. The graph is called as DAG (directed acyclic graph). In such graphs the vertices can be ordered from ancestor to the descendants in the decreasing order of the finish time to give the topological sort for the graph.

This can be done by pushing the vertex as soon as they finish to a stack array. Then returning reverse of the stack array after whole dfs is performed on graph, as the descendants vertices will be add before the ancestor.

Basically Topological sort represents the order in which a set of vertices need to be accessed to reach the desired vertex, usually representing the dependencies of the vertex. A cycle in the graph prevents to define this dependency graph or ordering because of the chicken or the egg problem.

The above template can be updated to return the topological order of the graph, If no cycles else return True.

visited = defaultdict(bool)
# dTime refers to discovery time
dTime = defaultdict(int)
# fTime refers to finish time
fTime = defaultdict(int)
timer = 0

topOrder = []

# returns True if there is a cycle in the graph
def dfs(u: int)->bool:
  visited[u] = True
  # record the time/order in which the vertex was added to the recursive call stack
  timer += 1
  dTime[u] = timer
  for v in graph[u]:
    if v not in visited:
      if dfs(v):
        return True
    else:
      # v node already visited, now checking if it is a ancestor in dfs tree, by checking if it is finished
      if v not in fTime:
        return True
  # record the time/order in which the vertex pops out of the recursive call stack
  timer += 1
  fTime[u] = timer
  # append the finished vertex to the stack to get the topological order, as descendants will always finish before the ancestors.
  # So this will be in the increasing order of finish time.
  topOrder.append(u)
  return False

# Outer loop to run dfs on each non visited vertex, If cycles no top order can be found, return early
for v in graph:
  if v not in visited:
    if dfs(v):
      return []

# print topological order by reversing the vertices in the stack. i.e. decreasing order of finish time.
topOrder.reverse()
return topOrder

• Course Schedule

In this problem, the courses and prerequisites relationship is given. All the courses cannot be taken if there is a cycle in the graph as a dependency graph for each node cannot be obtained. So the problem is about detecting cycle in the graph.

I have the templated above, I have replaced fTimer with a finish map which is just keeping track of whether is finished or not by bool. As a back edge as seen earlier will be only be there between the vertex (node) and the neighbor (v) which is visited by not finished as it is the ancestor.

def canFinish(self, n: int, prerequisites: List[List[int]]) -> bool:
    adjList = defaultdict(list)

    for e in prerequisites:
        # Making edge as e[1] -> e[0], e[0] depends on course e[1], can reach e[0] only from e[1]
        # reversing the direction of the edge from e[0] -> e[1] in adjList, doesn't really matter cycle will still be detected.
        # Only the topological order will be reversed.
        adjList[e[1]].append(e[0])

    # dfs to return True if graph at node has cycles else return false.
    def dfs(node: int) -> bool:
        visited[node] = True
        for v in adjList[node]:
            if v not in visited:
                if dfs(v):
                    # cycle in a graph at vertex v return True.
                    return True
            else:
                # Back edge check, if visited but not finished.
                if v not in finish:
                    # Found back edge, cycle detected return True
                    return True

        finish[node] = True
        return False

    # Keep track of finished nodes in the recursive tree.
    finish = defaultdict(bool)
    visited = defaultdict(bool)
    for node in range(n):
        if node not in visited:
            if dfs(node):
                return False

    return True

• Course Schedule II

This problem extends the previous problem, apart from detecting cycles also need to return the finish order in reverse, which is also the topological order of the graph.

def findOrder(self, n: int, prerequisites: List[List[int]]) -> List[int]:
    adjList = defaultdict(list)

    for e in prerequisites:
        # Making edge as e[1] -> e[0], e[0] depends on course e[1], can reach e[0] only from e[1]
        # reversing the direction of the edge from e[0] -> e[1] in adjList, doesn't really matter cycle will still be detected.
        # Only the topological order will be reversed, so if done that no reverse needs to be done at the end.
        adjList[e[1]].append(e[0])

    # dfs to return True if graph at node has cycles else return false.
    def dfs(node: int) -> bool:
        visited[node] = True
        for v in adjList[node]:
            if v not in visited:
                if dfs(v):
                    # cycle in a graph at vertex v return True.
                    return True
            else:
                # Back edge check, if visited but not finished.
                if v not in finish:
                    # Found back edge, cycle detected return True
                    return True

        # Node finished the recursive call, mark it as finished True.
        finish[node] = True
        finishOrder.append(node)
        return False

    # Keep track of the finish order, in topological from descendent to ancestor
    finishOrder = []
    # Keep track of finished nodes in the recursive tree.
    finish = defaultdict(bool)
    visited = defaultdict(bool)
    for node in range(n):
        if node not in visited:
            if dfs(node):
                return []
    # reverse to the get the finish order from ancester to descendent
    finishOrder.reverse()
    return finishOrder

BFS#