Intervals

In this article will talk about the interval problems, and look for pattern in such problems. In interval problems a sequence of overlapping and non-overlapping intervals are given denoted by [start, end] time on the number line.

Example such problems

• Merge Intervals

An interval is defined by a range by two points, start and end both inclusive. An overlap of two intervals can be seen in four ways, if one of the interval is taken as a reference. For example, if red interval is taken as reference.

1. Red interval starts before blue interval s1 <= e2 and e1 >= s2.
2. Red interval is contained by blue interval such that s1 <= e2 and e1 >= s2
3. Red Interval contains blue interval such that s1 <= e2 and e1 >= s2
4. Red Interval ends after blue interval s1 <= e2 and e1 >= s2

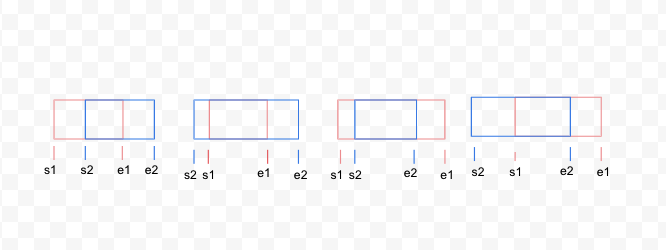
Basically all these 4 types of overlap can be indentified by just one condition s1 <= e2 and e1 >= s2. Which means if one of the interval starts before the other interval’s end and same interval end after the start of the other interval then both the intervals overlap. Once it is found that there is an overlap, intervals can merged to a new interval as:

newMergedInterval = [min(s1, s2), max(e1, e2)]

If all the intervals are layed down on the number line in sorted order. It would be easier to do merge them one by one. So based on that the algorithm can be given as.

1. Sort the intervals based on the (start, end)
2. Create an empty stack
3. Iterate over the sorted intervals.
4. Check if there is any interval on top of the stack which overlap with current interval.
   • If yes merge it, and update top of the stack.
5. Else just add the current interval to the stack.
6. Return the stack.

Time complexity of the algorithm can be given as O(NlogN) and Space as O(N).

st = 0 # start index
end = 1 # dnd index
def merge(intervals: List[List[int]]) -> List[List[int]]:
    intervals = sorted(intervals)
    n = len(intervals)
    res = []
    for i in range(n):
        if res and intervals[i][st] <= res[-1][end] and res[-1][end] >= intervals[i][st]:
            # Overlap: Merge with the top of the stack interval with current interval
            res[-1][st] = min(res[-1][st], intervals[i][st])
            res[-1][end] = max(res[-1][end], intervals[i][end])
        else:
            res.append(intervals[i])
    return res

• Insert Interval

Using the template of the above problem, the insert interval problem can be solved. By taking the inserted interval as the initial interval in the stack. In this problem an extra condition needs to be added for the case when the given interval is after the current interval. This case can be checked using condition e1 > e2. In such cases the top interval needs to be popped first and then inserted after the current interval.

Note: Sorting is not needed in this because intervals are given as sorted. This give a time and space complexity of O(N) .

st = 0
end = 1
def insert(intervals: List[List[int]], newInt: List[int]) -> List[List[int]]:
    res = [newInt]
    n = len(intervals)
    for i in range(n):
        if res and res[-1][st] <= intervals[i][end] and res[-1][end] >= intervals[i][st]:
            # Overlap: Merge with the top of the stack interval with current interval
            res[-1][st] = min(res[-1][st], intervals[i][st])
            res[-1][end] = max(res[-1][end], intervals[i][end])
        elif res and res[-1][end] > intervals[i][end]:
            # interval on top of the stack is after the current interval
            top = res.pop()
            res.append(intervals[i])
            res.append(top)
        else:
            res.append(intervals[i])
    return res

If the intervals were not sorted, then the inserted interval could be added to the intervals and sort them and run the merge algorithm afterwards as given above. In that case sorting itself would have taken O(NlogN) algorithm.